meProp: Sparsified Back Propagation for Accelerated Deep Learning with Reduced Overfitting
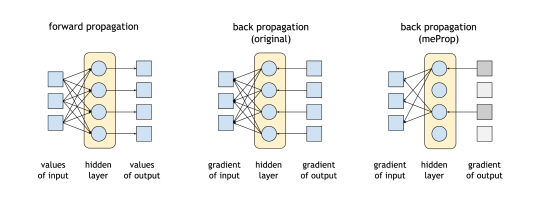 An illustration of meProp.
An illustration of meProp.Abstract
We propose a simple yet effective technique for neural network learning. The forward propagation is computed as usual. In back propagation, only a small subset of the full gradient is computed to update the model parameters. The gradient vectors are sparsified in such a way that only the top-k elements (in terms of magnitude) are kept. As a result, only k rows or columns (depending on the layout) of the weight matrix are modified, leading to a linear reduction (k divided by the vector dimension) in the computational cost. Surprisingly, experimental results demonstrate that we can update only 1–4% of the weights at each back propagation pass. This does not result in a larger number of training iterations. More interestingly, the accuracy of the resulting models is actually improved rather than degraded, and a detailed analysis is given.